2021. 7. 11. 22:23ㆍ개발/알고리즘
이전에 백준 사이트에서 에라토스테네스의 체 문제를 푼적이 있다. 자료구조를 공부해보고 싶어서 종만북 2권을 보는데 첫번째 장에서 비트마스크를 통한 에라토스테네스의 체를 구현한 부분이 있어서 블로깅 해본다.
비트마스크는 bit연산을 통해 문제를 해결하는 방법을 말한다.
[알고리즘/자바] 백준 2960번 - 에라토스테네스의 체
2960번: 에라토스테네스의 체 2, 4, 6, 8, 10, 3, 9, 5, 7 순서대로 지워진다. 7번째 지워진 수는 9이다. www.acmicpc.net 주어진 N이 소수라면 2보다 크거나 같고 N보다 작은 수로 나눠 떨어지면 안된다. ( 주어
soojong.tistory.com
아래는 종만북을 학습하고 있는 과정에서 작성한 글이기 때문에 오류가 있을수 있으니 수정해야할 부분 있으면 댓글 달아주세요.
비트마스크를 사용해 0부터 7까지 숫자의 소수를 구하려고 한다면 단 8bit만 있으면 된다.

C++ 코드를 통해서 어떤식으로 0,1을 각 비트에 표시하는지 살펴보자.
구현하기
전역변수로 sieve(체) 배열과 int N을 선언한다. N은 소수를 구하고자하는 숫자 범위를 의미한다. 아래 코드에서 N을 10으로 셋팅했기때문에 0부터 9까지 존재하는 소수를 뽑아낼 것이다. sieve 배열의 사이즈는 (N+ 7) / 8 이라는 연산에 의해 결정된다.

Q. 나누기 8을하는 이유는??
A. 나누기 8은 배열의 크기를 결정하기 위해 사용한다. unsigned char가 8bit 데이터 타입이기 때문에 (N+7)이 15인 경우 소수를 표시하기위해 적어도 2개 index가 필요한다. 따라서 나누기 8 연산을 통해서 2개 index를 확보한다. ( 8bit x 2 = 16bit 확보 )
Q. +7을 하는 이유는?
A. 8로 나눴을때 몫을 +1하기 위함이다. N이 3일때를 생각해보자. +7 연산 없이 N을 8로 나눠버리면 어떤 index도 확보되지 않는다. ( 몫이 0이기 때문에 ) 하지만 +7을 해줌으로써 몫이 +1 되면서 1개의 index(8bit)를 확보 할수 있게된다.
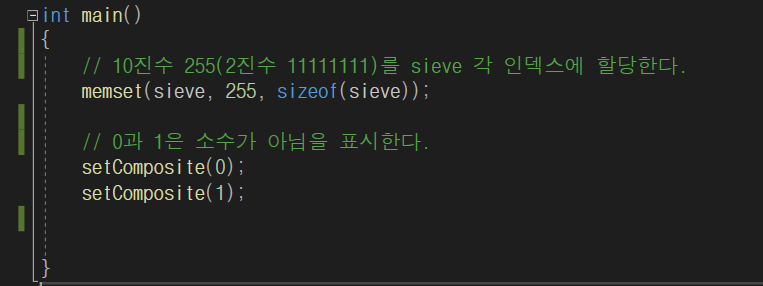
main을 구현한다. sieve 배열의 데이터를 10진수 255로 셋팅한다.

현재의 sieve 배열상태는 아래와 같다. 현재 상태만 보면 0부터 15까지 모두 소수라고 표시되어 있다. 이 상태에서 소수가 아닌 수를 나타내는 bit를 찾아 0으로 변경해야한다.

setComposite 함수를 통해 0번째 bit와 1번째 bit는 setComposite 함수를 통해서 소수가 아님(0으로 셋팅)을 표시한다.
setComposite함수 코드는 아래와 같다.

k가 0인 경우의 동작을 살펴보자.
0 & 7 연산을 수행하면 모든 bit가 0이 된다. 따라서 1<< 0연산을 수행하게 되는데 1을 0번 shift하기 때문에 1<<0의 결과는 00000001이다. 이를 not 연산하면 11111110이 된다. 여기서 sieve[0]과 & 연산을 수행하게 되는데 그 결과 11111110이 된다. k가 0으로 입력된 경우 0번째 bit만 0으로 셋팅됨을 확인할 수 있다. ( k가 1인 경우 1번째 bit가 0으로 변경된다. ) 즉, setComposite함수는 k bit 번째를 0으로 셋팅하는 역할을 한다.
이제 2 ~ N-1까지 숫자 사이에 존재하는 소수가 아닌수를 찾아보자. 코드는 아래와 같이 구현한다.
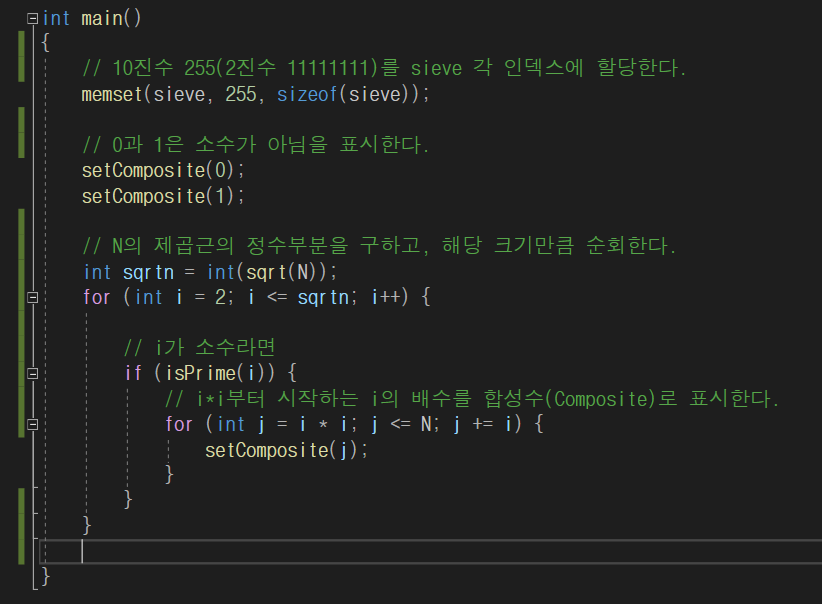
Q. N이 아닌 N의 제곱근까지만 for문을 수행하는 이유는??
A. i부터 N의 제곱근까지 수행을하는데 for문 내에서 i의 제곱에 대한 소수 구분 처리를 하기 때문이다.
Q. 왜 i가 아닌 i*i부터 시작하는가?
A. i * i 미만의 i의 배수는 모두 소수 구분 처리가 완료되었다.
중간에 i가 소수인지 판단하는 isPrime이라는 함수가 보이는데 구현은 아래와 같이 한다.

k가 3인 경우를 생각해보자.
k & 7 연산을 수행하면 2진수 0000 0011이 된다. 0000 0011은 10진수로 3을 의미하기 때문에 1을 3만큼 left shift 수행한다. 결과는 0000 1000이 된다. 그리고 sieve[k>>3]과 & 연산을 수행한다. k>>3은 k를 8로 나눈것과 같기 결국 sieve[0]의 값과 & 연산을 수행해야한다. 올바르게 에라토스테네스의 체를 구현했다면 k가 4 인 경우 sieve[0]의 값은 1010 1100이 되어있어야 한다.( Why? k가 2인 경우를 작업할때 2의 배수는 모두 소수가 아닌것으로 표기가 되었을 것이다. 따라서 자연수 4,6을 의미하는 5번째 bit와 7번째 bit가 0으로 표기된다. ) 1010 1100과 00001000을 & 연산하면 0000 1000이 때문에 isPrime 함수는 true를 반환된다.
k=4인 경우도 수행해보자.
k & 7 연산을 수행하면 2진수 0000 0100이 된다. 0000 0100은 10진수로 4를 의미하기 때문에 1을 4만큼 left shift 수행한다. 결과는 0001 0000이 된다. 그리고 sieve[0]과 & 연산을 수행한다. 올바르게 에라토스테네스의 체를 구현했다면 k가 4가 들어왔을때 sieve[0]의 값은 1010 1000이 되어 있어야한다. sieve[0]의 값인 1010 1000과 0001 0000을 &연산을 수행하면 0000 0000이라는 값이 나오게 된다.
bitset을 통해서 seieve 내용을 확인한다.
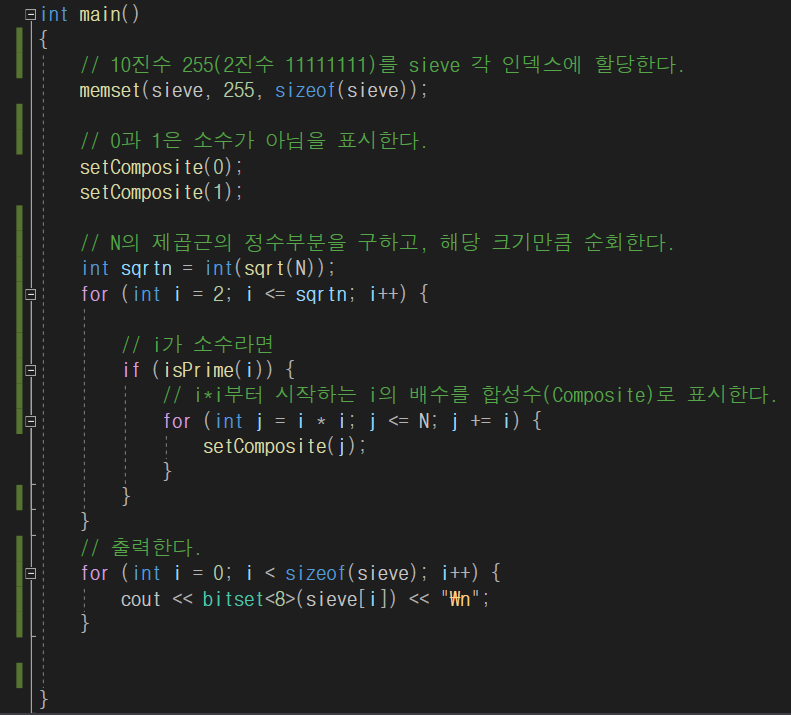
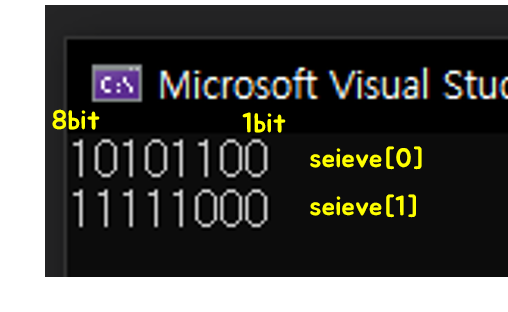
출력결과는 아래와 같다. N을 10으로 설정하고 실행했기 때문에 sieve[1]의 3bit까지만 소수여부를 판단했으며 이후 bit는 초기값인 1로 채워져있다. N을 16으로 설정했다면 16bit를 모두 활용해서 결과를 확인해 볼 수 있었을것이다.
'개발 > 알고리즘' 카테고리의 다른 글
| [알고리즘/자바] 백준 2941번 - 크로아티아 알파벳 (0) | 2021.07.26 |
|---|---|
| [알고리즘/자바] 백준 5622번 - 다이얼 (0) | 2021.07.14 |
| [알고리즘/자바] 백준 2164번 - 카드2 (0) | 2021.05.28 |
| [알고리즘/자바] 백준 9252번 - LCS 2 (2) | 2021.01.28 |
| [알고리즘/자바] 백준 4811 - 알약 (0) | 2021.01.21 |